Olá pessoal, hoje vamos implementar um algoritmo para verificar se o número é um quadrado perfeito e listar os dez primeiro, será utilizada a IDE PyCharm para nosso exemplo.
Podemos observar que um número quadrado perfeito possui um padrão de formação, onde n é um número inteiro positivo:
n² = n . n = a
1² = 1 . 1 = 1
2² = 2 . 2 = 4
3² = 3 . 3 = 9
4² = 4 . 4 = 16
5² = 5 . 5 = 25
6² = 6 . 6 = 36
7² = 7 . 7 = 49
8² = 8 . 8 = 64
9² = 9 . 9 = 81
10² = 10 . 10 = 100
Uma das formas para descobrirmos se um número é quadrado perfeito é verificando se o número possui raiz quadrada exata. Para realizarmos esse algoritmo, temos de saber que um número elevado a 1/2 é igual à raiz quadrada.
Com essas informações, crie um script com o nome quadradoPerfeito.py
Digite o código abaixo.
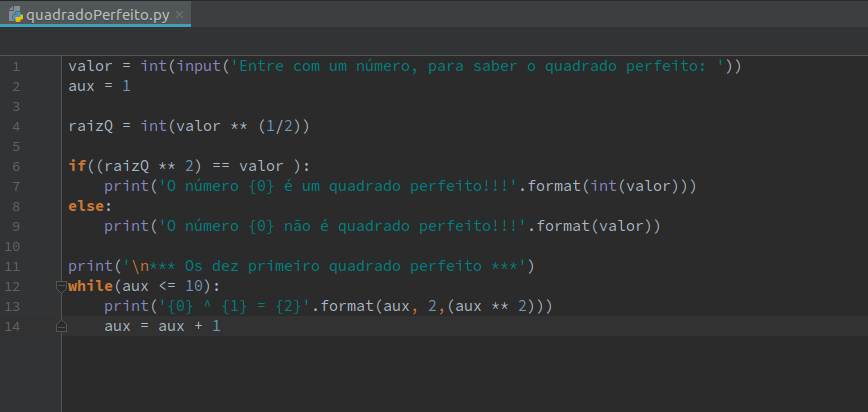
| valor = int(input('Entre com um número, para saber o quadrado perfeito: ')) | |
| aux = 1 | |
| raizQ = int(valor ** (1/2)) | |
| if((raizQ ** 2) == valor ): | |
| print('O número {0} é um quadrado perfeito!!!'.format(int(valor))) | |
| else: | |
| print('O número {0} não é quadrado perfeito!!!'.format(valor)) | |
| print('\n*** Os dez primeiro quadrado perfeito ***') | |
| while(aux <= 10): | |
| print('{0} ^ {1} = {2}'.format(aux, 2,(aux ** 2))) | |
| aux = aux + 1 |
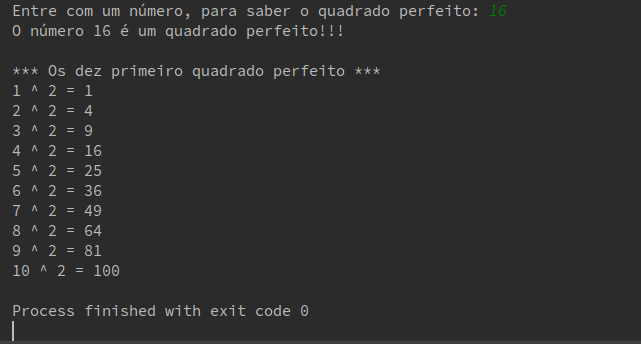
Pronto, o resultado será exibido como esperado após a execução :)
Referências
OLIVEIRA, Naysa Crystine Nogueira. “Número quadrado perfeito”; Brasil Escola. Disponível em https://brasilescola.uol.com.br/matematica/numero-quadrado-perfeito.htm. Acesso em 15 de janeiro de 2018.